
TOUR EBIKE
L'acquisto della Ebike (9 giugno 2020 ) per festeggiare l'ultimo giorno di lavoro e la pensione ha dischiuso nuovi orizzonti. Se prima di allora la MTB è stata utilizzata solo per tenersi in forma soffrendo non poco difronte alle inevitabili salite, il mezzo motorizzato mi ha permesso di raggiungere luoghi oltre la linea degli eventi.
La presenza di un numero quasi infinito di forestali specie in Trentino - Alto Adige permette all'escursionista di raggiungere mete in tempi relativamente brevi, rispetto a quanto sarebbe possibile a piedi e senza faticare troppo.
Il tempo a disposizione per il fotografo appassionato quale reputo essere, si dilata, per cui gli itinerari con la Ebike diventano a loro volta itinerari fotografici esattamente come accadeva e accade ancor oggi nelle escursioni a piedi.
In ogni caso è opportuno ribadire che per ogni obiettivo che uno si prefigge, esiste il mezzo appropriato e le grandi altezze sono un privilegio di chi ama camminare.

Colterenzio: 9 giugno 2020
L'uso della Ebike porta con sé dei limiti derivanti dalla necessità di rendere minimo l'ingombro, anche quello relativo al set fotografico; ecco allora che le fotografie sono state eseguite per lo più col cellulare che quanto a qualità è molto lontano dalla inseparabile compatta e dalla pesante reflex.
Non avendo la necessità di stamparle, ma solo di pubblicarle su web, la qualità scadente non costituisce un problema.
La tabella che segue riporta gli itinerari principali a partire dal 2020, di cui per alcuni è reperibile la scheda completa di tutte le informazioni che ho pensato di allegare.
Osservo che i chilometri totali relativi a tali itinerari sono meno del 50% di quanto effettivamente percorso durante l'anno considerato. Questo significa che ho utilizzato la bici anche intorno a casa e che alcuni itinerari comunque impegnativi non li ho documentati anche perchè affrontati più volte in passato e spesso a bordo della MTB che oggi utilizzo solo lungo le ciclabili che affiancano l'Adige e l'Isarco e dunque in piano, sperando nell'assenza di vento.
Più interessante è la cifra del dislivello totale pari a circa 16.000 metri per il solo 2022; a titolo d'informazione è un terzo di quello affrontato dai professionisti del ciclismo, solo che loro poveretti, lo concentrano in 21 giorni.......non lo dicono, ma un quintale di antidolorifici e antinfiammatori sono posti sul loro comodino.
Tanto di cappello per gli atleti di uno sport duro che a quei livelli non giova particolarmente alla salute dell'organismo.
LINK:
BREVI CONSIDERAZIONI SUL MOTO DEI GRAVI E MENO GRAVI A BORDO DELLA EBIKE EVITANDO L'OSPEDALE
Riporto di seguito alcune definizioni e considerazioni che riguardano il moto a bordo della bicicletta in particolare in discesa.
La prima definizione è il concetto di pendenza che ovviamente è strettamente legato all'angolo di inclinazione della strada.
 .
.
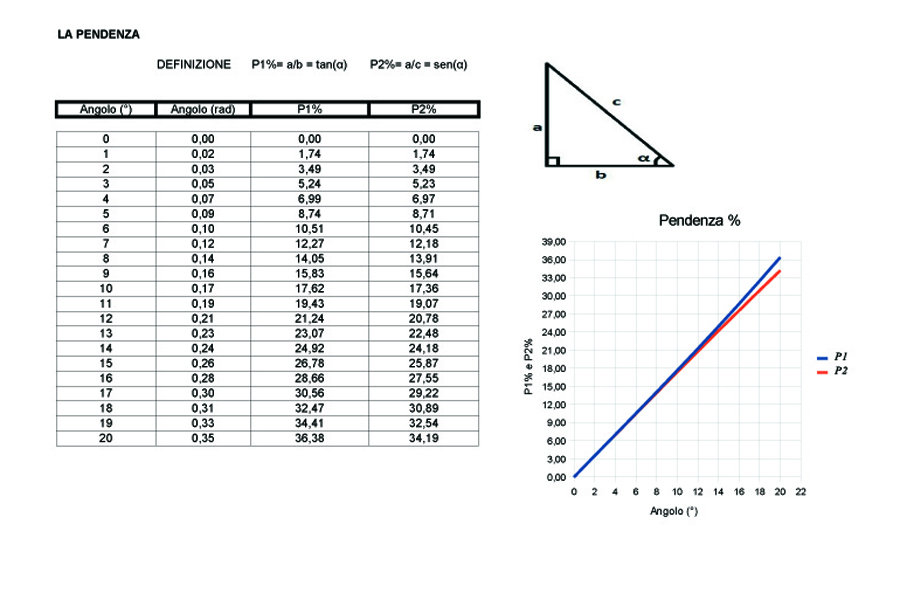
Angolo di inclinazione e pendenza
La tabella di Excel riporta nella prima colonna l'angolo in gradi, nella seconda quello in radianti e successivamente la definizione classica che usa la funzione trigonometrica tangente nonchè quella più utile che utilizza la funzione seno. Perchè più utile? Perchè il ciclista di fatto si muove sull'ipotenusa "c" e non sale lungo il cateto "a". La cosa interessante è che le due funzioni tangente e seno danno risultati quasi identici per angoli inferiori a 20°. Si badi bene che la pendenza in questo caso è del 35% ossia altissima e non affrontabile in salita da nessun ciclista.
I due tornanti della chiesa di Caupo hanno pendenze pari a circa il 20% corrispondenti ad un angolo pari a 12° e vi garantisco che dopo un giro sul Grappa il ritorno a casa consiglia all'atleto attempato di impostare il programma turbo e proseguire speditamente fino a casa senza soffrire ulteriormente.
Un altro concetto interessante è quello relativo alla scomposizione della forza peso di un grave che si muove lungo un piano inclinato:
Il piano inclinato e la scomposizione delle forze
Geniale fu l'intuizione di Galileo Galilei: con il piano inclinato si ha la possibilità di modificare l'accelerazione che subisce un grave. Se con α = 90° siamo in presenza dell'accelerazione di gravità g, con un angolo minore l'accelerazione cala con la legge del sen (α) fino a ridursi a zero se il piano diventa orizzontale. In questo caso la reazione del vincolo è uguale e contraria al peso del grave ossia al prodotto m*g e non vi è alcuna componente orizzontale per cui il "ciclista " sta fermo ed in equilibrio sul piano.
La domanda che spesso si pone quando scendiamo lungo una strada è la seguente: la velocità del ciclista è legata alla sua massa? In altri termini scende più velocemente il ciclista più pesante?
Aristotele avrebbe risposto affermativamente ma ciò corrisponde alla verità solo in presenza di attrito come vedremo. Il ragionamente " astratto " che fece Galileo fu quello di immaginare due gravi di massa e forma diversa un sasso ed una piuma, lanciati dalla Torre di Pisa. In assenza di attrito e quindi dell'aria i due oggetti giungono a terra nello stesso istante perchè l'accelerazione g è la stessa per entrambi.
Il moto sarà quello naturalmente accelerato in cui la velocità continuerà a crescere con legge: v = g*t velocità che sarà quindi la stessa per i due oggetti.
Ciò vale anche per il piano inclinato dove al posto di g l'accelerazione effettiva sarà g*sen (α).
Ma come sappiamo gli attriti ci sono e guai se non ci fossero che cadremmo a terra esattamente come accade, calpestando la classica buccia di banana o camminando sulla superficie ghiacciata del lago di Braies dove molti dementi vogliono verificare non le leggi di scivolamento ma la tenuta del ghiaccio a fine aprile.
Dunque nel moto della bicicletta intervengono gli attriti e allora proviamo ad enumerarne alcuni:
L'ATTRITO DEL MEZZO OSSIA DELL'ARIA IN CUI CI MUOVIAMO
L'ATTRITO RADENTE ( DI STRISCIAMENTO ) DEI PNEUMATICI
L'ATTRITO VOLVENTE (DI ROTOLAMENTO) DEI PNEUMATICI
L'ATTRITO DEI MOZZI DELLE RUOTE
Dei quattro riportati il più importante in discesa è il primo ossia l'attrito dell'aria che fa sentire il suo effetto in prima approssimazione secondo il quadrato della velocità del ciclista ma non solo. E' noto infatti che assumendo una posizione aerodinamica si scende più velocemente, mentre esponendo tutto il torace all'aria si frena. La discesa da ponte delle Stue, sulla larga strada asfaltata del Manghem permette di verificare tutto questo e altro ancora.
Come è logico quindi, la forma aerodinamica influisce sul moto e sulla velocità di discesa.
Per essere più precisi la resistenza del mezzo che si oppone al moto dipende da quattro fattori:
DENSITA' DELL'ARIA
VELOCITA' DEL MOBILE
SUPERFICIE DELLA SEZIONE PRINCIPALE ORTOGONALE AL MOTO (SEZIONE MAESTRA)
FORMA DEL SOLIDO E DUNQUE DEL VALORE DEL COEFFICIENTE AERODINAMICO DELLO STESSO
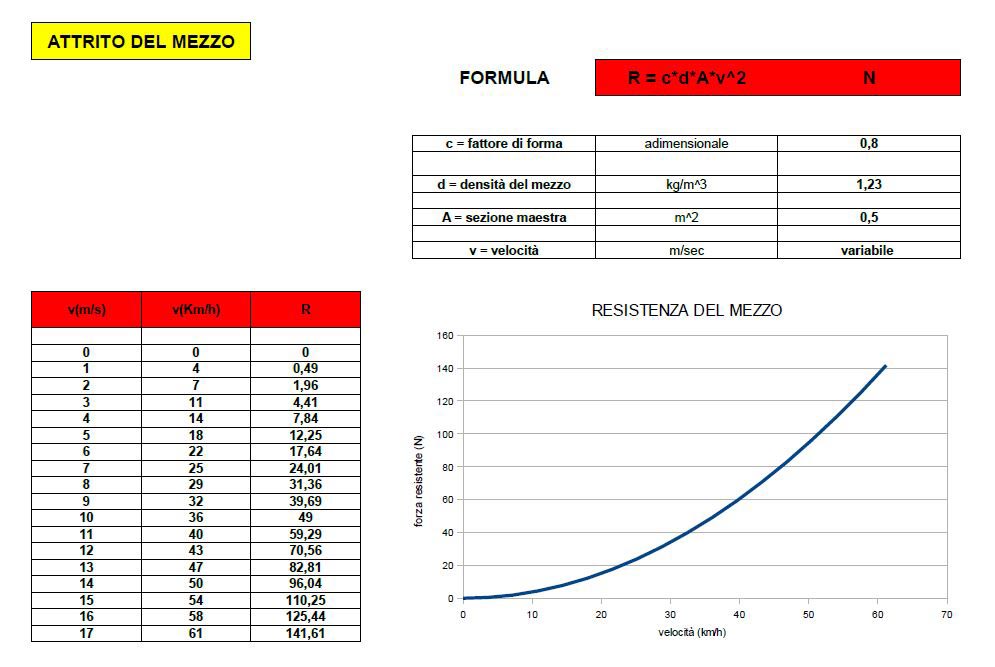
Grafico della Forza resistente
Il grafico risulta essere una parabola dato che R dipende dalla velocità al quadrato. Il fattore di forma o di areodinamicità è stato scelto pari a 0,8 mentre la sezione maestra pari a 0,5 m^2. La densità dell'aria è pari a 1.23 Kg/m^3 sul livello del mare. A parte questo ultimo parametro sia il coefficente "c" che la sezione maestra "A" dipendono da vari fattori come il tipo di ruota montato sulla bicicletta, dall'abbigliamento, il tipo di casco, dalle misure dell'atleta e dalla posizione assunta.
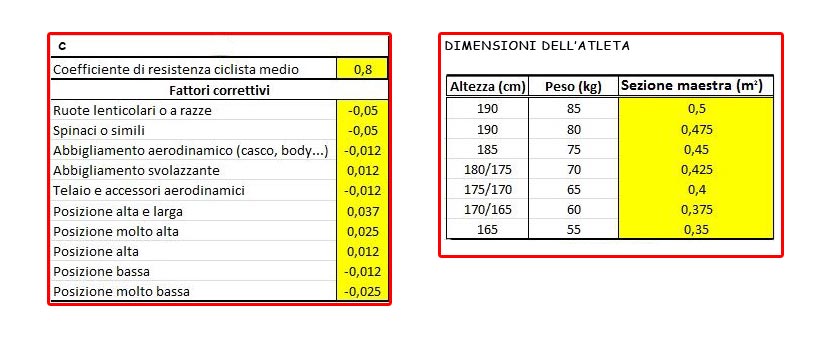
Fattori "c" e "A"
VELOCITA' LIMITE IN DISCESA
Conoscendo la massa dell'atleta e della bicicletta nonchè l'angolo di inclinazione della strada è possibile calcolare con una certa approsimazione la velocità limite che egli può raggiungere.
Se l'atleta pesa 70Kg e la bici 25Kg come nel caso di una Ebike, ipotizzando un angolo di 5° corrispondente ad una pendenza del 9% la forza di spinta senza pedalare risulta essere:
Fp= M g*sen (α) = 81N con M=95Kg
Analizzando il grafico della resistenza del mezzo si ricava che la velocità a cui corrisponde una forza resistente R = 81N è di circa 47km/h. A tale velocità la forza di spinta risulta uguale a quella resistente e il ciclista non accelerà più.
Tale velocità potrà essere superata modificando ad esempio la propria posizione sulla sella, la qual cosa produce sia una diminuzione del fattore di forma "c" che della sezione maestra "A".
NOTA:
Da quanto analizzato risulta dunque che la massa dell'atleta influisce sulla velocità del mezzo.....per cui aveva ragione Aristotele!
GRAFICO DELLA VELOCITA' LIMITE IN DISCESA
Uno degli argomenti di Fisica che mi ha appassionato di più è stato quello del comportamento di alcuni componenti elettronici ad un sollecitazione cosidetta " a gradino ". Cosa succede se un condensatore o un induttore posti in serie ad un resistore vengono alimentati da una batteria in corrente continua ?
Diciamo semplificando che " si caricano "; il primo accumula energia elettrostatica, il secondo energia magnetica. Se la cosa appare banale per un tecnico, l'analisi matematica che governa questi fenomeni non lo è affatto. Per descrivere in modo qualitativo il fenomeno bisogna saper risolvere un' equazione differenziale.
Peccato che all'università non ci fosse un corso dedicato a questa branca della matematica a cui Newton diede il principale contributo.
Lungi da essere un esperto in materia, per la soluzione di alcune equazioni differenziali si può ricorrere al calcolo numerico; dai differenziali si passa alle differenze finite e utilizzando una formula ricorsiva, una volta fissati i parametri normalmente costanti, si ricava la variabile che interessa, sia questa una tensione, una corrente o come nel nostro caso la velocità del ciclista in caduta libera.
L'aspetto interessante è dunque che equazioni differenziali formalmente simili descrivono processi che convolgono campi della fisica del tutto differenti.
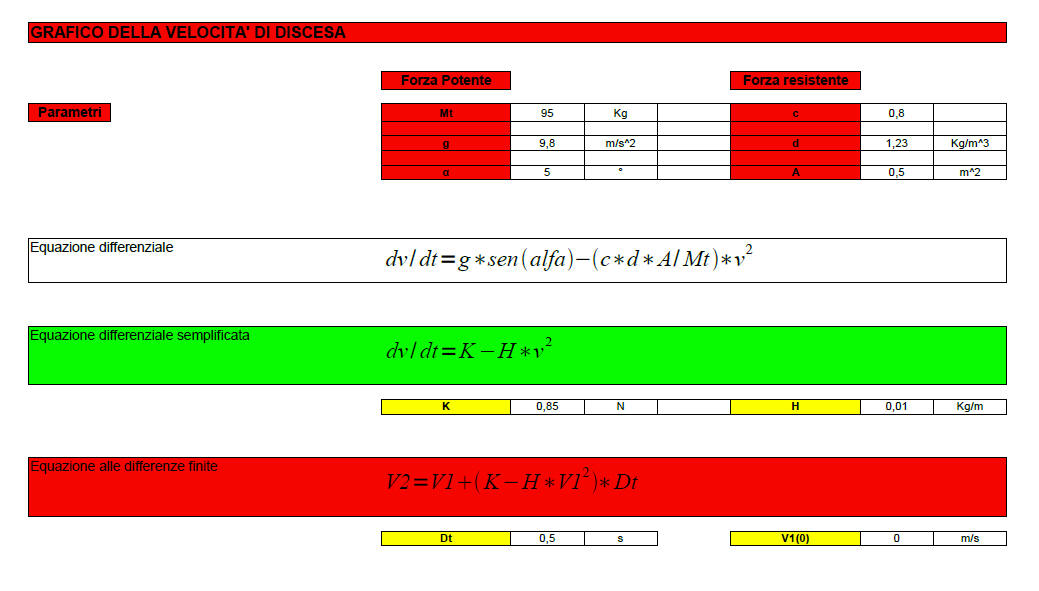
Parametri dell'equazione differenziale
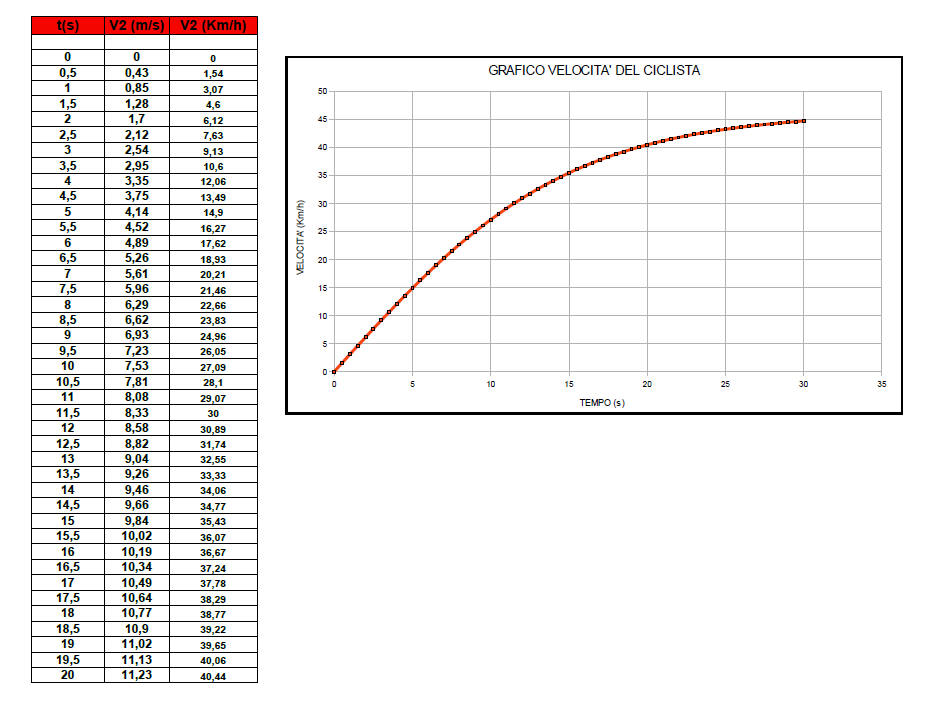
Grafico della velocità di discesa
Nota:
La tabella riporta solo alcuni dei dati necessari alla costruzione del grafico. Possiamo notare che la velocità limite è circa uguale a 45Km/h in accordo con quanto indicato nel paragrafo precedente dato che sono stati usati gli stessi parametri. Notiamo inoltre che inizialmente la velocità cresce linearmente dato che la resitenza del mezzo non fa sentire i suoi effetti. In altri termini il ciclista accelera ma ovviamente sempre di meno fino a raggiungere la velocità limite.
Per confronto riporto qui le curve di velocità relative a due " atleti " da 70 e 90 Kg. Mentre il parametro K risulta lo stesso, H risulta minore per l'atleta più pesante dato che la massa va a dividere. Ovviamente non si tiene conto né del diverso fattore di forma, né della diversa sezione maestra di norma entrambi più grandi per l'atleta più pesante fatto questo che riduce le differenze di velocità in discesa.
Tabella parametri
Velocità a confronto
L'atleta più pesante raggiunge dopo 50s una velocità di 50Km/h contro i 45Km/h di quello " più atletico ". Dunque per quanto riguarda la discesa la dieta è abolita!
Ma in salita è un'altra storia.
LA POTENZA DELLA BATTERIA DI UNA EBIKE
Gli anni passano e la nostra efficienza rimanendo nel campo atletico cala. Escludiamo eventuali malattie e auspichiamo un processo di invecchiamento graduale e sereno.
Tutto questo accade anche per la batteria della nostra bicicletta per cui l'energia che è in grado di fornire cala con il passare degli anni.
Le ditte che costruiscono batterie, forniscono un tasso di resa negativo pari a circa il 4-5%. Dopo l'ultimo giro in bici che ha comportato un dislivello di circa 1400 m ho voluto ragionare ( per quel che ne sono capace ) sui dati forniti dal computer di bordo. La potenza media consumata riferibile praticamente alla salita era di 125 W e la durata dell'ascesa fattore questo un po' impreciso era di circa 2,3 ore. In discesa ovviamente la batteria non erogava potenza. A giro concluso il computer indicava un residuo di batteria espresso in forma percentuale pari al 48%.
Ho realizzato la seguente tabelle che riporta la potenza della batteria in funzione degli anni; nello specifico la mia ha circa tre anni visto che siamo all'inizio della quinta stagione ciclo-turistica.
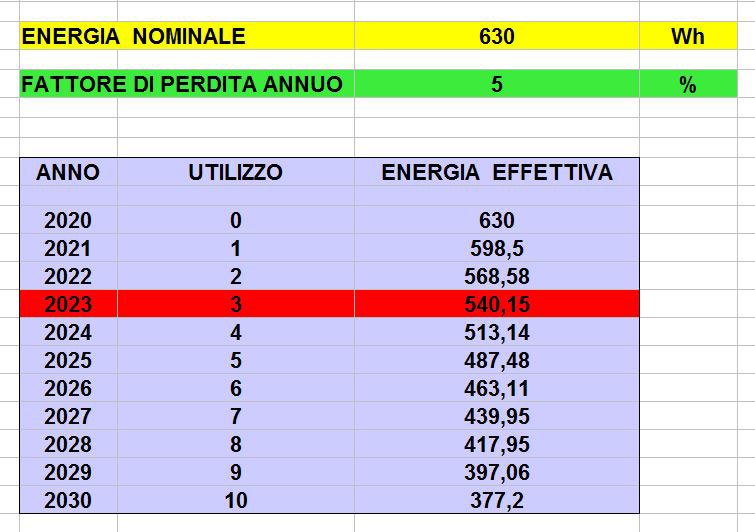
Tabella efficienza energetica
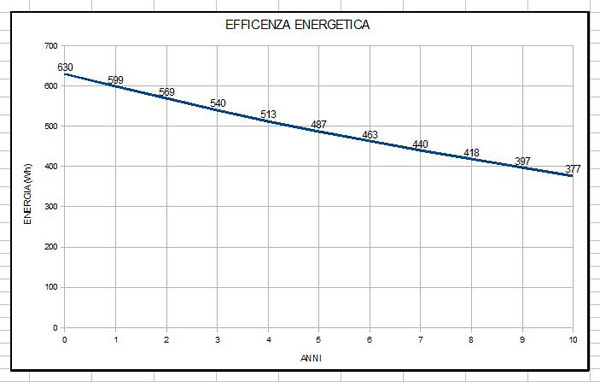
Grafico efficienza energetica
Analizzando il grafico che ha un andamento quasi rettilineo si nota in realtà un calo di efficienza più repentino all'inizio e minore con il passare degli anni.
Dai 630 Wh nominali del 2020 contando un tasso negativo di efficienza del 5% a fine 2023 (inizio 2024 ) ho approssimativamente a disposizione 540 Wh.
Che conti possiamo fare con i dati relativi all'ultimo giro?
Utilizzando la potenza media e le ore impiegate, possiamo calcolare l'energia consumata che risulta essere pari a 285 Wh.
Se come suggerisce la tabella, dispongo ad oggi di una batteria da 540 Wh, il residuo risulta essere pari a 255 Wh.
In forma percentuale dovrei allora disporre di un 47% di batteria, numero che non si discosta molto da quanto indicato dal computer di bordo, tenendo conto delle approssimazioni fatte.
Concludendo se oggi volessi ritentare l'impresa di arrivare a Caupo partendo da Compostela affrontare di nuovo il Redebus sarebbe rischioso e non basterebbero le due ore di ricarica di allora per centrare l'obiettivo.